UOMOP
Logistic Regression(이진 분류 로지스틱 회귀) 본문
Logistic Regression(로지스틱 회귀)는 분류 알고리즘이다. (회귀 알고리즘이 아니다.)
회귀의 특성으로 임의의 값(z)가 도출되지만, z를 시그모이드 함수를 통해서 확률로 변환하여 양성클래스(1)에 대한 확률을 도출하게 된다.
우선, target 클래스가 2개인 이진 분류 로지스틱 회귀에 대해 알아보도록 한다.
import pandas as pd
fish_df = pd.read_csv("http://bit.ly/fish_csv_data")
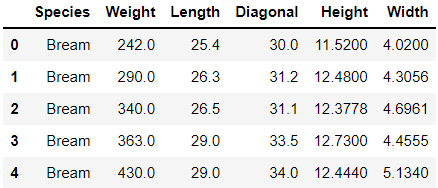
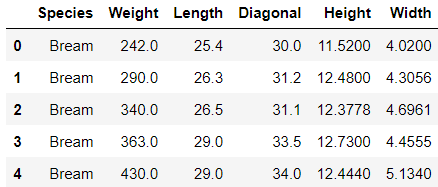
fish_df.head()우선, 웹에서 csv파일을 read_csv메소드를 통해서 불러온다.
indexes = (fish_df["Species"] == "Bream") | (fish_df["Species"] == "Smelt")
only_bream_smelt = fish_df[indexes]
only_bream_smelt.head(5)fish_df에서 Species(종)이 "Bream(도미)", "Smelt(빙어)"만을 추출하기 위해서 index를 찾는 과정이다.
도미와 빙어의 인덱스에서만 True가 되도록 한 후 indexes라는 변수에 리스팅하였다.
이 후, 해당 row만을 추출하기 위해 only_bream_smelt = fish_df[indexes]로 코딩하였다.
위 DataFrame에서 Species가 target이 되고 나머지 특성들이 input이 된다.
# input data, target data 분리
target_df = only_bream_smelt["Species"]
input_df = only_bream_smelt.drop("Species", axis = 1)
# 모듈 호출
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
# 학습/검증 data 분리
train_input, test_input, train_target, test_target = train_test_split(input_df,
target_df, random_state = 42)
ss = StandardScaler()
# Scaling 정도 설계
ss.fit(train_input)
# Scaling
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
# 로지스틱 회귀로 훈련
lr.fit(train_scaled, train_target)print(lr.predict(train_scaled[:5]))['Bream' 'Bream' 'Bream' 'Smelt' 'Smelt']
train_scaled의 data를 통해서 예측을 진행해본 결과 [도미 도미 도미 빙어 빙어]
print(lr.predict_proba(train_scaled[:5]))[[0.97784567 0.02215433]
[0.95707934 0.04292066]
[0.98232085 0.01767915]
[0.04075105 0.95924895]
[0.04518058 0.95481942]]
각 샘플 특성에 대한 0(음성 = Bream)일 확률과 1(양성 = Smelt)일 확률이 차례로 출력되었다.
예측 확률이 출력되는 순서는 0, 1순이고 앞 순의 알파벳이 0으로 할당된다.
print(lr.coef_, lr.intercept_)[[-0.57548931 -0.79284742 -0.82598773 -0.86627132 -0.82254687]] [-2.38253807]
로지스틱 회귀도 선형 함수를 학습하기 때문에 가중치와 절편을 확인해 보았다.
특성이 5개였으므로, 각 특성에 해당하는 가중치가 출력되었고, 마지막으로 절편이 출력되었다.
z = -0.57548931 * 무게 -0.79284742 * 길이 -0.82598773 * 대각선 -0.86627132 * 높이 -0.82254687 * 두께 -2.38253807
라는 함수를 학습한 것이고, sample의 특성들이 대입되어 z가 도출된다.
샘플마다 z를 구할 수 도 있다.
decisions = lr.decision_function(train_scaled[:5])
print(decisions)[-3.78731874 -3.104533 -4.01753203 3.15866903 3.05085494]
train_scaled에 있는 5개 샘플들에 대한 z값을 출력해보았다.
위 z값을 시그모이드 함수에 대입하여 도출되는 값이 양성클래스(1)에 확률이다.
밑에서 메소드를 통해서 확인해보도록 하자.
from scipy.special import expit # 시그모이드 함수를 호출
print(expit(decisions))[0.02215433 0.04292066 0.01767915 0.95924895 0.95481942]
decisions 변수에 5개 샘플에 대한 z가 있고, 이를 expit에 넣어서 양성클래스(1)에 대한 확률을 확인해보았다.
0이 도미, 1이 빙어 이므로
[도미 도미 도미 빙어 빙어]
가 출력되는 것을 확인할 수 있었다.
'Ai > ML' 카테고리의 다른 글
| 확률적 경사 하강법(Stochastic Gradient Descent) (0) | 2022.01.27 |
|---|---|
| Logistic Regression(다중 분류 로지스틱 회귀) (0) | 2022.01.27 |
| Multiple Regression(다중 회귀) - 릿지/라쏘 (0) | 2022.01.25 |
| Linear Regression(선형 회귀) (0) | 2022.01.25 |
| k-최근접 이웃 model의 문제점 (0) | 2022.01.25 |
Comments