UOMOP
Multiple Regression(다중 회귀) - 릿지/라쏘 본문
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
df = pd.read_csv("https://bit.ly/perch_csv")
df.head()perch_all = df.to_numpy()
print(perch_all.shape)(56, 3)
perch_weight = np.array(
[5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0,
110.0, 115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0,
130.0, 150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0,
197.0, 218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0,
514.0, 556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0,
820.0, 850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0,
1000.0, 1000.0]
)
perch_weight = perch_weight.reshape(-1, 1)
print(perch_weight.shape)(56, 1)
input data, target data를 모두 불러왔다.
3개의 특성이 있는 input data라는 것을 확인할 수 있고, 우선 특성 3개 만을 사용해서 선형 회귀 모델로 학습을 해보도록 한다.
3개 특성만을 이용하여 선형 회귀 모델로 학습
train_input, test_input, train_target, test_target = train_test_split(perch_all,
perch_weight, random_state = 42)
lr = LinearRegression() # 학습 모델 호출
lr.fit(train_input, train_target) # 학습
print("3가지 특성 훈련 셋의 결정계수 : {}".format(lr.score(train_input, train_target)))
print("3가지 특성 검증 셋의 결정계수 : {}".format(lr.score(test_input, test_target)))3가지 특성 훈련 셋의 결정계수 : 0.9559326821885706
3가지 특성 검증 셋의 결정계수 : 0.8796419177546366
기존에 있던 input data의 3가지 특성만을 사용해서 학습을 진행시킨 결과, 과적합 현상이 발생하였다.
더 좋은 성능을 위해서 특성을 늘려보도록 한다.
다중회귀 (특성 9개)
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures()
poly.fit(train_input)
train_poly = poly.transform(train_input)
test_poly = poly.transform(test_input)
print(poly.get_feature_names())['x0', 'x1', 'x2', 'x0^2', 'x0 x1', 'x0 x2', 'x1^2', 'x1 x2', 'x2^2']
PolynomialFeatures를 통해서 기존 특성 3개를 이용하여 9개 특성이 되도록 조합하였다.
이 input data를 통해서 학습을 진행시켜보고 결정계수 값을 확인해보도록 한다.
lr.fit(train_poly, train_target)
print("9가지 특성 훈련 셋의 결정계수 : {}".format(lr.score(train_poly, train_target)))
print("9가지 특성 검증 셋의 결정계수 : {}".format(lr.score(test_poly, test_target)))9가지 특성 훈련 셋의 결정계수 : 0.9903183436982125
9가지 특성 검증 셋의 결정계수 : 0.9714559911594094
다중 회귀를 통해서 더 좋은 성능이 도출되었다. 그렇다면 특성의 수를 더 늘리면 더 좋아지는지 확인해보자.
다중회귀 (특성 55개)
poly = PolynomialFeatures(degree = 5, include_bias = False)
poly.fit(train_input)
train_poly5 = poly.transform(train_input)
test_poly5 = poly.transform(test_input)
print(train_poly5.shape)(42, 55)
55개 특성으로 재조합된 것을 확인할 수 있다.
lr = LinearRegression()
lr.fit(train_poly5, train_target)
print("55가지 특성 훈련 셋의 결정계수 : {}".format(lr.score(train_poly5, train_target)))
print("55가지 특성 검증 셋의 결정계수 : {}".format(lr.score(test_poly5, test_target)))55가지 특성 훈련 셋의 결정계수 : 0.9999999999938143
55가지 특성 검증 셋의 결정계수 : -144.40744532797535
특성의 갯수를 많이 늘리면 극도로 과도 적합되는 것을 확인할 수 있었다.
규제를 통해서 극도의 과도 적합 문제를 해결해보도록 하자.
규제 모델은 가중치(기울기)를 작게 하는 원리이다. 대표적으로 릿지 회귀, 라쏘 회귀가 있다.
가중치를 줄일 때 "릿지 회귀"의 경우, 가중치의 제곱만큼을 완화시키고
"라쏘 회귀"의 경우, 가중치의 절댓값만큼을 완화시킨다.
또한 규제 모델은 Scaling Preprocessing 과정이 꼭 필요하다.
Ridge Regression(릿지 회귀)
from sklearn.linear_model import Ridge
from sklearn.preprocessing import StandardScaler
# Scaling
ss = StandardScaler()
ss.fit(train_poly5)
train_poly5_scaled = ss.transform(train_poly5)
test_poly5_scaled = ss.transform(test_poly5)
ridge = Ridge()
ridge.fit(train_poly5_scaled, train_target)
print("Scaling을 한 후, 55가지 훈련 셋의 결정계수 : {}".format(ridge.score(train_poly5_scaled, train_target)))
print("Scaling을 한 후, 55가지 검증 셋의 결정계수 : {}".format(ridge.score(test_poly5_scaled, test_target)))Scaling을 한 후, 55가지 훈련 셋의 결정계수 : 0.9896101671037343
Scaling을 한 후, 55가지 검증 셋의 결정계수 : 0.979069397761539
과적합 문제가 많이 해결된 것을 확인할 수 있다.
하지만, 규제 모델을 호출할 때 alpha 값을 설정하여 더 좋은 모델을 설계할 수 있다.
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]
train_score = []
test_score = []
for i in alpha_list :
ridge = Ridge(alpha = i)
ridge.fit(train_poly5_scaled, train_target)
train_score.append(ridge.score(train_poly5_scaled, train_target))
test_score.append(ridge.score(test_poly5_scaled, test_target))
import matplotlib.pyplot as plt
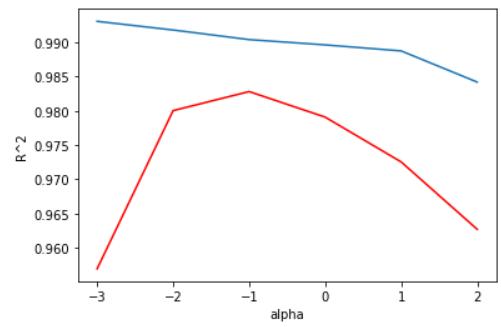
plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score, color = "r")
plt.xlabel("alpha")
plt.ylabel("R^2")
plt.show()alpha가 0.1일 때 두 결정계수가 비교적 높으면서 차이가 거의 없는 것을 확인할 수 있다.
alpha를 0.1로 설정하고 다시 확인해보도록 한다.
ridge = Ridge(alpha = 0.1)
ridge.fit(train_poly5_scaled, train_target)
print("alpha가 0.1인 릿지 모델을 통해 확인해본 55특성 훈련 셋의 결정계수 : {}".format(ridge.score(train_poly5_scaled, train_target)))
print("alpha가 0.1인 릿지 모델을 통해 확인해본 55특성 검증 셋의 결정계수 : {}".format(ridge.score(test_poly5_scaled, test_target)))alpha가 0.1인 릿지 모델을 통해 확인해본 55특성 훈련 셋의 결정계수 : 0.9903815817570368
alpha가 0.1인 릿지 모델을 통해 확인해본 55특성 검증 셋의 결정계수 : 0.9827976465386954
성능이 훨씬 좋아진 것을 확인하였다.
Lasso Regression(라쏘 회귀)
from sklearn.linear_model import Lasso
lasso = Lasso()
lasso.fit(train_poly5_scaled, train_target)
print("라쏘 모델을 통해 확인해본 55개 특성 훈련 셋의 결정계수 : {}".format(lasso.score(train_poly5_scaled, train_target)))
print("라쏘 모델을 통해 확인해본 55개 특성 검증 셋의 결정계수 : {}".format(lasso.score(test_poly5_scaled, test_target)))라쏘 모델을 통해 확인해본 55개 특성 훈련 셋의 결정계수 : 0.989789897208096
라쏘 모델을 통해 확인해본 55개 특성 검증 셋의 결정계수 : 0.9800593698421884
라쏘 모델 또한 alpha값을 설정하여 더 좋은 모델을 설계해보도록 하자.
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]
train_score = []
test_score = []
for i in alpha_list :
lasso = Lasso(alpha = i)
lasso.fit(train_poly5_scaled, train_target)
train_score.append(lasso.score(train_poly5_scaled, train_target))
test_score.append(lasso.score(test_poly5_scaled, test_target))
import matplotlib.pyplot as plt
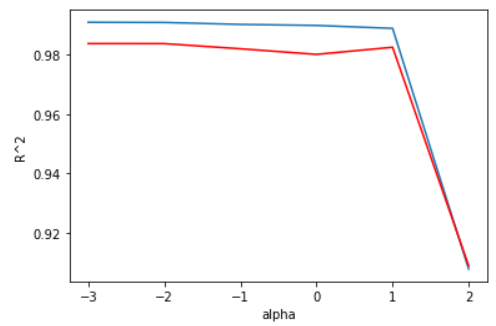
plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score, color = "r")
plt.xlabel("alpha")
plt.ylabel("R^2")
plt.show()lasso 규제 선형 모델의 경우, alpha가 10일 때 최고 성능을 보여주고 있다.
alpha를 10으로 고정하여 학습을 해보도록 한다.
lasso = Lasso(alpha = 10)
lasso.fit(train_poly5_scaled, train_target)
print("alpha가 10인 라쏘 모델을 통해 확인해본 55특성 훈련 셋의 결정계수 : {}".format(lasso.score(train_poly5_scaled, train_target)))
print("alpha가 10인 라쏘 모델을 통해 확인해본 55특성 검증 셋의 결정계수 : {}".format(lasso.score(test_poly5_scaled, test_target)))alpha가 10인 라쏘 모델을 통해 확인해본 55특성 훈련 셋의 결정계수 : 0.9888067471131867
alpha가 10인 라쏘 모델을 통해 확인해본 55특성 검증 셋의 결정계수 : 0.9824470598706695
라쏘 모델의 특징은 모든 특성을 사용하지 않는다는 것이다. 55개의 특성 중 몇 개의 특성을 사용했는지 확인해보도록 한다.
print(np.sum(lasso.coef_ == 0))40
55개 중 40개의 특성은 사용하지 않고 있다. 15개만 사용하였다.
'Ai > ML' 카테고리의 다른 글
| Logistic Regression(다중 분류 로지스틱 회귀) (0) | 2022.01.27 |
|---|---|
| Logistic Regression(이진 분류 로지스틱 회귀) (0) | 2022.01.27 |
| Linear Regression(선형 회귀) (0) | 2022.01.25 |
| k-최근접 이웃 model의 문제점 (0) | 2022.01.25 |
| 농어(perch) 무게 예측 using "k-최근접 이웃 회귀" (0) | 2022.01.24 |
Comments